Predicting mobile app retention with logistic regression
Introduction
Hello! In today’s post, I’ll delve into a popular topic in mobile app analytics: predicting user retention. My example will be quite straightforward. I’ll use one of the most accessible and least complex machine learning models: logistic regression. Of course, there are many other approaches to modeling retention, but this post will focus on one that is beginner-friendly and doesn’t require extensive skills or knowledge to apply. Personally, I often use logistic or linear regression in my work, as they’re simple yet effective tools for solving many problems. I hope this post will be helpful to you!
Let’s get to work! 🚀
About User Retention
User retention is a metric that measures the ability of an app, website, or digital product to keep users engaged over time. It reflects the percentage of users who return to the product after their initial interaction, typically tracked over specific time frames such as daily, weekly, or monthly.
Why focus on user retention?
- Improve long-term engagement: High retention rates indicate that users find value in your app, encouraging sustained usage and engagement.
- Reduce churn: Understanding retention patterns helps identify reasons why users might leave, enabling proactive improvements to prevent churn.
- Enhance monetization: Retained users are more likely to make purchases, engage with premium features, or generate revenue through ads.
- Build a loyal user base: Retention fosters loyalty, increasing the likelihood of recommendations and organic growth.
- Optimize user acquisition ROI: Retaining users ensures a better return on investment for marketing efforts, as acquiring new users is often more costly than keeping existing ones engaged.
How to measure user retention?
User retention is often calculated as the percentage of users who return to the app within a specific time frame, such as Day 1, Day 7, or Day 30. A common formula is:
Retention Rate (%)=(Number of users who initially joinedNumber of users active on a specific day)×100
In my analysis, I will focus on Week 1 retention, specifically measuring the percentage of users who return to the app during the second week after using it in their first week.
About Logistic Regression
Logistic regression is a widely used statistical model in machine learning for binary classification tasks. In the context of user retention, logistic regression helps predict whether a user will return to the app after a specific period (e.g., after one week), based on their attributes and behavior during their first week of using the app.
Unlike linear regression, which predicts continuous outcomes, logistic regression predicts probabilities, outputting values between 0 and 1. These values represent the likelihood that an event will occur—in this case, whether a user will return to the app or not.
Why use logistic regression?
- Simplicity: Logistic regression is easy to understand and implement, making it an ideal starting point for many analysts and data scientists.
- Interpretability: The model produces coefficients that represent the impact of each feature on the likelihood of retention, making it easy to interpret which factors are most important.
- Efficiency: Logistic regression works well with smaller datasets and is computationally less expensive compared to more complex models.
- Binary outcome: It’s particularly suitable for binary outcomes like retention prediction, where the goal is to classify users as “returning” or “not returning.”
Logistic regression works by calculating the odds of a user returning to the app. The odds are derived from a linear combination of the input features, and then transformed using a logistic (sigmoid) function to ensure the output is between 0 and 1, which can be interpreted as a probability.
When to use logistic regression for retention analysis?
- When you want to predict the likelihood that a user will return to your app based on their behavior or characteristics.
- When you have a clear, binary outcome, such as “retained” vs. “not retained” users.
- When you’re dealing with a relatively simple dataset and need a model that’s easy to implement and interpret.
Logistic regression is often a powerful yet simple tool for predicting user retention
Generating sample data
Since I don’t have access to real data—and even if I did, sharing it might not be possible—I’ll create a synthetic dataset using Python and the Pandas library.
Let’s imagine a simple fitness app. The app struggles with retaining users: more than 60% don’t return after their first week of using it. The product manager is trying to figure out why. Guessing is hard because there could be many factors:
- External factors: Like new, strong competitors entering the market.
- Internal factors: For example, a feature that doesn’t work properly or isn’t user-friendly.
But it’s not all negative! We can also identify positive factors — features that are working well and significantly contribute to user retention. This is critical information for the team managing the app. Highlighting these successful features could help optimize the onboarding experience and guide users toward them during their first week.
The fitness app includes several basic features:
- Logging workouts
- Tracking meals
- Healthy recipes
- Setting goals
- Wellness challenges
- Adding friends and interacting with them
Additionally, the app sends notifications and collects basic user data, such as gender and age.
These features and user attributes will serve as input variables for building our logistic regression model. Normally, we would first conduct an exploratory data analysis on the app’s data and, based on that, select the most important features for the model. However, here we’re working with significant simplifications, as this post is just an example.
Let’s create a synthetic dataset.
np.random.seed(42)
num_users = 30000
age = np.random.normal(32, 6, num_users).astype(int)
age = np.clip(age, 18, 60)
age[age > 40] = np.random.choice(np.arange(18, 40), size=np.sum(age > 40))
gender = np.random.choice(['Female', 'Male'], size=num_users, p=[0.5, 0.5])
fitness_level = np.random.choice(['Beginner', 'Intermediate', 'Advanced'],
size=num_users,
p=[0.6, 0.3, 0.1])
workouts = np.random.poisson(lam=3, size=num_users)
workouts = np.clip(workouts, 0, 7)
meals = np.random.poisson(lam=10, size=num_users)
meals = np.clip(meals, 0, 40)
added_friends = np.random.choice([0, 1], size=num_users, p=[0.9, 0.1])
set_goals = np.random.choice([0, 1], size=num_users, p=[0.2, 0.8])
push_enabled = np.random.choice([0, 1], size=num_users, p=[0.8, 0.2])
challenge_participation = np.random.choice([0, 1], size=num_users, p=[0.7, 0.3])
recipes_used = np.random.choice([0, 1], size=num_users, p=[0.9, 0.1])
retention_prob = (
0.00 * (fitness_level == 'Beginner') +
0.00 * (fitness_level == 'Intermediate') +
0.00 * (fitness_level == 'Advanced') +
0.0 * age +
0.0 * (gender == 'Female') +
0.0 * (gender == 'Male') +
0.15 * workouts / 7 +
0.27 * meals / 40 +
0.8 * added_friends +
0.01 * set_goals +
0.4 * push_enabled +
0.25 * challenge_participation +
0.4 * recipes_used
)
retention = np.random.binomial(1, np.clip(retention_prob, 0, 1))
df = pd.DataFrame({
'age': age,
'gender': gender,
'fitness_level': fitness_level,
'workouts': workouts,
'meals': meals,
'added_friends': added_friends,
'set_goals': set_goals,
'push_enabled': push_enabled,
'challenge_participation': challenge_participation,
'recipes_used': recipes_used,
'retention_week_1': retention
})
As you can see, I have manually set the influence of various features on the probability of a “1” appearing in the retention field for the following week. From this, you can immediately deduce what the conclusions from the data analysis will be, but I can’t make it in the better way.
Let’s take a look at the first 5 records of the generated dataset:
df.head()
| index | age | gender | fitness_level | workouts | meals | added_friends | set_goals | push_enabled | challenge_participation | recipes_used | retention_week_1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 34 | Female | Beginner | 3 | 4 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 31 | Male | Beginner | 2 | 9 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 35 | Female | Intermediate | 2 | 14 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | 35 | Female | Intermediate | 2 | 11 | 0 | 1 | 1 | 0 | 0 | 0 |
| 4 | 30 | Female | Beginner | 5 | 15 | 0 | 1 | 0 | 0 | 0 | 0 |
And now let’s see how the values are distributed in the retention_week_1 field:
df["retention_week_1"].value_counts()
| retention_week_1 | count |
|---|---|
| 0 | 18104 |
| 1 | 11896 |
Less than 40% of users returned to the app during the first week.
Data modeling
The first step is to encode non-numeric fields. In our dataset, these are fitness_level and gender. We’ll use one-hot encoding for this purpose. One-hot encoding converts categorical variables into binary columns, where each category is represented as a 1 or 0. This method avoids assigning arbitrary numerical values to categories, which could mislead the model. It’s particularly useful for logistic regression, as it ensures proper treatment of categorical data without implying any ordinal relationship.
df_encoded = pd.get_dummies(df, columns=['gender', 'fitness_level'], drop_first=True)
df_encoded = df_encoded.astype(int)
Now, I will split the dataset into the feature matrix (X) and the target vector (y). The feature matrix contains all the descriptive variables, while the target vector includes the variable being predicted—retention in the first week.
X = df_encoded.drop('retention_week_1', axis=1)
y = df_encoded['retention_week_1']
Next, we will apply a StandardScaler to the numerical continuous variables in the feature matrix. Standardizing continuous variables scales them to have a mean of 0 and a standard deviation of 1. This ensures that all features contribute equally to the logistic regression model, preventing variables with larger ranges (e.g., age or number of meals) from dominating the model’s coefficients.
columns_to_scale = ['age', 'workouts', 'meals']
scaler = StandardScaler()
X[columns_to_scale] = scaler.fit_transform(X[columns_to_scale])
Now, let’s check for multicollinearity by creating a correlation heatmap and performing a Variance Inflation Factor (VIF) analysis. Multicollinearity occurs when features are highly correlated with each other, which can lead to instability in the logistic regression model and make the coefficients difficult to interpret. The heatmap will provide a visual representation of the correlations between features, helping us identify any strong relationships. VIF analysis complements this by quantifying how much the variance of each regression coefficient is inflated due to multicollinearity. If we find features with high VIF values (typically above 5 or 10), it may indicate a need to remove or combine those features to improve the model’s stability and interpretability.
sns.heatmap(X.corr(), cmap='Greens')

vif = pd.DataFrame()
vif["Features"] = X.columns
vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(vif)
| Features | VIF |
|---|---|
| age | 1.000235 |
| workouts | 1.000167 |
| meals | 1.000622 |
| added_friends | 1.102732 |
| set_goals | 3.732310 |
| push_enabled | 1.226512 |
| challenge_participation | 1.390908 |
| recipes_used | 1.105465 |
| gender_Male | 1.882767 |
| fitness_level_Beginner | 3.225051 |
| fitness_level_Intermediate | 2.109078 |
The analysis shows that all features have VIF values well below the common thresholds of 5 or 10, indicating that multicollinearity is not a major concern in this dataset. All features can be safely used in the model without causing instability due to multicollinearity.
Now, we’ll use Mutual Info Score to measure how much each feature shares information with our target variable, retention in the first week. This helps us identify the most informative features, allowing us to simplify the model and improve its performance by focusing on the variables that matter most.
mi_scores = {}
for col in X.columns:
mi_scores[col] = metrics.mutual_info_score(X[col], y)
mi = pd.DataFrame(mi_scores.items(), columns=['Feature', 'Mutual_Info_Score'])
mi = mi.sort_values(by='Mutual_Info_Score', ascending=False)
print('Ranked Features based on Mutual Information Score:\n', mi)
| Feature | Mutual_Info_Score |
|---|---|
| added_friends | 8.254964e-02 |
| push_enabled | 4.337057e-02 |
| recipes_used | 2.302765e-02 |
| challenge_participation | 2.235452e-02 |
| workouts | 2.998782e-03 |
| meals | 1.085953e-03 |
| age | 2.837636e-04 |
| set_goals | 1.173846e-04 |
| fitness_level_Intermediate | 2.921707e-06 |
| gender_Male | 8.047385e-07 |
| fitness_level_Beginner | 2.831308e-07 |
| The Mutual Info Scores show that added_friends is the most informative feature for predicting retention, followed by push_enabled and recipes_used. Features like workouts, meals, and age contribute less, while set_goals, fitness_level, and gender are the least informative for retention prediction. |
Now, we can move on to creating the model. First, we split the dataset into training and test sets. Then, we create the model, using the default class balancing method since we have fewer users who returned to the app. There are other ways to balance classes, such as SMOTE, but for simplicity, we’ll stick with this approach.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = LogisticRegression(max_iter=1000, class_weight="balanced")
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print("Accuracy:", "%.2f" % metrics.accuracy_score(y_test, y_pred) )
print("Precision:", "%.2f" % metrics.precision_score(y_test, y_pred))
print("Recall:", "%.2f" % metrics.recall_score(y_test, y_pred))
print("F1 Score:", "%.2f" % metrics.f1_score(y_test, y_pred))
print("AUC:", "%.2f" % metrics.roc_auc_score(y_test, y_pred))
cm = metrics.confusion_matrix(y_test, y_pred, labels = model.classes_)
cmap = 'Greens'
disp = metrics.ConfusionMatrixDisplay(confusion_matrix = cm,display_labels = model.classes_)
disp.plot(cmap=cmap)
Precision: 0.68
Recall: 0.73
F1 Score: 0.70
AUC: 0.75
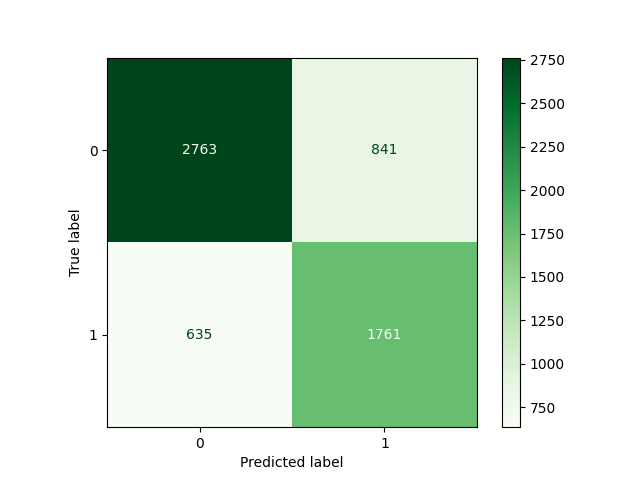
The model’s performance metrics are as follows:
- Accuracy: 0.75 – The model correctly predicts 75% of the total instances. While a good baseline, accuracy may be misleading if the data is imbalanced.
- Precision: 0.68 – Among the instances predicted as having high retention, 68% were correct. This is important in scenarios where false positives (predicting retention when the user won’t return) are costly.
- Recall: 0.73 – Of all the actual cases with high retention, the model correctly identified 73%. Recall is crucial when it’s important to capture as many true positives as possible, even at the risk of some false positives.
- F1 Score: 0.70 – The F1 score balances precision and recall. With a value of 0.70, the model has a decent trade-off between identifying retention users and avoiding false predictions.
- AUC: 0.75 – The Area Under the Curve (AUC) of 0.75 indicates the model has a good ability to distinguish between users who will and won’t return to the app, with a value close to 1 meaning strong predictive power.
I think the model performs quite well. Of course, in a real-world scenario, there would likely still be room for improvement, especially with more data and fine-tuning. However, the goal of this model is to optimize the performance of a mobile app, not to achieve perfect prediction accuracy. Unlike medical or financial applications, where high precision and recall are critical, in this case, a model that accurately predicts user retention with reasonable metrics is valuable for improving user experience and app engagement.
Let’s evaluate the importance of each feature in the model by examining the coefficients. We extract the coefficients and pair them with the feature names to create a DataFrame. By adding the absolute values of the coefficients, we can easily see which features have the most impact on the model, whether positive or negative. Sorting them helps us identify the most influential features in predicting user retention.
coefficients = model.coef_[0]
features = X.columns
feature_importance = pd.DataFrame({'Feature': features, 'Coefficient': coefficients})
feature_importance['Abs_Coefficient'] = feature_importance['Coefficient'].abs()
feature_importance = feature_importance.sort_values(by='Abs_Coefficient', ascending=False)
print('Feature Importance (Most to least):\n', feature_importance)
| Feature | Coefficient | Abs_Coefficient |
|---|---|---|
| added_friends | 4.690906 | 4.690906 |
| recipes_used | 2.020701 | 2.020701 |
| push_enabled | 2.016600 | 2.016600 |
| challenge_participation | 1.359809 | 1.359809 |
| workouts | 0.236286 | 0.236286 |
| set_goals | 0.109489 | 0.109489 |
| meals | 0.092486 | 0.092486 |
| fitness_level_Intermediate | 0.040248 | 0.040248 |
| fitness_level_Beginner | 0.037985 | 0.037985 |
| age | -0.012937 | 0.012937 |
| gender_Male | 0.010622 | 0.010622 |
| From the feature importance table, we can draw the following conclusions: |
added_friendshas the highest absolute coefficient, indicating it is the most influential feature in predicting user retention. The positive coefficient suggests that having friends added increases the likelihood of retention.recipes_usedandpush_enabledalso have relatively high coefficients, meaning they play a significant role in retention. Both features have positive coefficients, suggesting that using recipes and having push notifications enabled both positively impact retention.challenge_participationis another important feature, with a moderate coefficient, indicating that engaging in challenges also improves retention.- Features like
workouts,set_goals, andmealshave smaller coefficients, meaning their impact on retention is less significant, but still positive. fitness_level_Intermediateandfitness_level_Beginnershow relatively small effects, with very low coefficients, indicating that a user’s fitness level has minimal influence on retention in this model.ageandgender_Malehave very small coefficients, suggesting these features have a negligible impact on the model’s ability to predict retention.
Overall, the features that encourage social interaction (e.g., added_friends, challenge_participation) and engagement (e.g., recipes_used, push_enabled) appear to have the most impact on retention.
Suggested strategy to increase retention:
To improve user retention, the app could focus on the following strategies:
-
Enhance Social Features:
Encourage users to connect with friends and participate in challenges. This can be done by making it easier to add friends, perhaps through social media integration, and promoting group challenges or competitions within the app. -
Boost User Engagement:
Focus on increasing the usage of features that promote content interaction, like recipes or health tips. Additionally, sending personalized push notifications based on user activity could keep users more engaged. -
Support Goal Setting:
Continue promoting the use of goal-setting features, as they have a moderate impact on retention. Consider adding more customizable goal options or progress-tracking features to help users feel more invested in their health journey. -
Target Specific User Groups:
While demographic features like age and gender showed little impact, the app could still experiment with personalized content for different user groups, particularly in the form of tailored fitness plans or meal suggestions. -
Simplify Onboarding and Early Engagement:
Given that social interaction and engagement are critical for retention, streamlining the onboarding process and encouraging new users to add friends, set goals, and explore recipes right away could increase the chances of long-term retention.
By focusing on these areas, the app can increase user satisfaction, engagement, and retention over time.
Conclusion
I hope you found this post insightful. Of course, in a real-world setting, things are rarely this clear-cut. There are many other factors and metrics to consider, and the impact of changes is often more subtle. Sometimes, improving retention is about making incremental gains rather than drastic shifts. The key takeaway is that testing new features and changes, and making decisions based on solid data analysis, is essential for long-term success. See you in the next post!