A/B testing of a new mobile app feature - example of the analysis
Introduction
Hello. In today’s post, I’ll be walking you through an example of step-by-step data analysis using an A/B test conducted in a mobile app. For the analysis, I’ll be using classic Python tools like Pandas, NumPy, or SciPy. Considering that the previous post was about data analysis from a UI/UX app survey, this can already be considered a mini-series on mobile app analytics.
Let’s get to work!
About A/B tests
A/B testing is a method of comparing two versions of the same element to determine which one performs better. In the context of mobile apps, A/B testing allows you to experiment with different UI elements, features, content, marketing strategies, and more to see which version has a better impact on user behavior, such as clicks, conversions, engagement, and retention.
Why conduct A/B testing in mobile apps?
- Improve conversion rates: A/B testing helps identify UI elements, features, or content that lead to higher conversion rates, such as purchases, registrations, or form completions.
- Increase engagement: A/B testing allows you to test different versions of content, buttons, layouts, and other elements to see which ones better engage users and keep them using the app longer.
- Optimize retention: A/B testing can help determine which features or marketing strategies lead to higher user retention, meaning users coming back to the app more often.
- Data-driven decision-making: A/B testing is data-driven, not guesswork, allowing you to make more informed decisions about app development and marketing strategies.
- Competitive advantage: Regularly conducting A/B testing can give your company an edge over the competition by allowing you to adapt more quickly to user preferences and market trends.
In summary, A/B testing is a valuable tool for mobile app developers and marketers that helps optimize the user experience, increase conversions, engagement, and retention, and make better business decisions.
A/B Test Assumptions
Imagine a simple grocery shopping list app. We previously introduced a product suggestion module to help users complete their shopping lists. This module was based on product popularity, suggesting items frequently purchased by other users. Unfortunately, this solution didn’t perform as expected. The module wasn’t very accurate, and users weren’t particularly interested in it. Time for a change! We decided to completely revamp the product suggestion module, harnessing the power of machine learning.
The new module operates quite differently. Instead of relying on product popularity, it considers a multitude of factors, including:
-
User purchase history: The module analyzes a user’s past purchases and suggests relevant items based on their shopping habits.
-
Seasonality: The module understands that summer calls for ice cream and refreshing drinks, while winter brings cravings for mulled wine and nuts. It accordingly suggests products aligned with the current season.
Significant effort went into creating this new module. We don’t want to rush its implementation like the previous version. Therefore, we’ve decided to conduct an A/B test on a smaller user group first. This will allow us to assess whether the change enhances feature effectiveness and translates to greater overall app engagement.
The goal of this A/B test is to compare the performance of the new machine learning-powered product suggestion module against the previous popularity-based module. We’ll evaluate the impact of both modules on conversion (adding products from the modules), average user session duration, and first-day retention.
Hypotheses:
-
Hypothesis 1: The new machine learning-powered product suggestion module will lead to higher conversion (adding products from the modules) compared to the previous module.
-
Hypothesis 2: The new machine learning-powered product suggestion module will engage users more, leading to longer sessions.
-
Hypothesis 3: The new machine learning-powered product suggestion module will make a better impression on new users and increase first-day retention.
Of course, in the real world, it’s worth analyzing more factors. We should check if introducing feature A, for instance, hasn’t negatively impacted the performance of feature B or the entire app. We need to monitor crash and error rates, negative reviews and feedback, monetization metrics, and more. In contrast, it’s crucial not to overanalyze and get bogged down in data while maintaining a balance between user satisfaction and business goals.
Additional Considerations:
-
Sample size: Ensure the sample size is large enough to provide statistically significant results.
-
Randomization: Randomly assign users to either the control group (old module) or the treatment group (new module) to eliminate bias.
-
Duration: Run the test for a sufficient period to gather enough data and make informed conclusions.
-
Monitoring and analysis: Continuously monitor the test’s progress and analyze the results to identify any trends or patterns.
-
Actionable insights: Use the test results to make data-driven decisions about the future of the product suggestion module.
By carefully planning and executing an A/B test, we can gain valuable insights into the effectiveness of our new product suggestion module and make informed decisions that ultimately improve the user experience and achieve our business objectives.
This post is just a quick, simple example, but I hope it’s helpful. Let’s move on!
Generating Sample Data
Of course, I don’t have a real application of this type, so I need to create sample data. This can be done very easily using Python. We will try to create a table that is a kind of event log that you may have to deal with using, for example, data generated by Google Analytics. Our example table will only contain the following fields:
- event_date - date of the event occurrence
- event_name - event name, we only generate two: product_suggestion_click and session_start
- user_id - user identifier
- test_group - A/B test group to which the user was classified
- event_params - event parameters, for the start of the session it will be the session duration and for clicking on product suggestions the product identifier
In the real world, such a table contains much more fields and the range of events performed by users is much wider. Since we want to get meaningful A/B test results, the table must favor the test group - it will have twice the probability of clicking on product suggestions, longer sessions and a higher probability of generating a session by the user the day after generating a conversion.
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import random
np.random.seed(42)
random.seed(42)
num_users = 1000
num_days = 30
test_groups = ['Baseline', 'Variant']
event_names = ['product_suggestion_click', 'session_start']
def random_date(start, end):
return start + timedelta(
seconds=random.randint(0, int((end - start).total_seconds())),
)
def generate_events(user_id, start_date, end_date, num_events, test_group_weights):
events = []
test_group = np.random.choice(test_groups, p=test_group_weights)
for _ in range(num_events):
event_date = random_date(start_date, end_date)
if test_group == 'Baseline':
event_name = random.choices(event_names, weights=[1, 1], k=1)[0]
session_duration = random.randint(30, 1800)
else:
event_name = random.choices(event_names, weights=[2, 1], k=1)[0]
session_duration = random.randint(1800, 3600)
if event_name == 'product_suggestion_click':
event_params = {'product_id': random.randint(1, 100)}
elif event_name == 'session_start':
event_params = {'session_duration_in_sec': session_duration}
events.append({
'event_date': event_date,
'user_id': user_id,
'test_group': test_group,
'event_name': event_name,
'event_params': event_params
})
if test_group == 'Variant' and random.random() < 0.2:
next_day = event_date + timedelta(days=1)
if next_day <= end_date:
session_duration = max(1, int(np.random.normal(avg_session_duration, 20)))
events.append({
'event_date': next_day,
'user_id': user_id,
'test_group': test_group,
'event_name': 'session_start',
'event_params': {'session_duration_in_sec': session_duration}
})
elif test_group == "Baseline" and random.random() < 0.1:
next_day = event_date + timedelta(days=1)
if next_day <= end_date:
session_duration = max(1, int(np.random.normal(avg_session_duration, 20)))
events.append({
'event_date': next_day,
'user_id': user_id,
'test_group': test_group,
'event_name': 'session_start',
'event_params': {'session_duration_in_sec': session_duration}
})
return events
start_date = datetime.now() - timedelta(days=num_days)
end_date = datetime.now()
data = []
test_group_weights = [0.5, 0.5]
for user_id in range(1, num_users + 1):
num_events = random.randint(1, 20)
user_events = generate_events(user_id, start_date, end_date, num_events, test_group_weights)
data.extend(user_events)
df = pd.DataFrame(data)
df['event_date'] = pd.to_datetime(df['event_date'])
The beginning of such a table should look like this:
| index | event_date | user_id | test_group | event_name | event_params |
|---|---|---|---|---|---|
| 0 | 2024-06-08 19:08:42.181455 | 1 | Baseline | session_start | {‘session_duration_in_sec’: 531} |
| 1 | 2024-06-18 10:03:53.181455 | 1 | Baseline | product_suggestion_click | {‘product_id’: 87} |
| 2 | 2024-07-04 01:24:13.181455 | 1 | Baseline | product_suggestion_click | {‘product_id’: 5} |
| 3 | 2024-06-09 00:43:18.181455 | 1 | Baseline | product_suggestion_click | {‘product_id’: 65} |
| 4 | 2024-06-08 20:55:19.181455 | 2 | Variant | product_suggestion_click | {‘product_id’: 84} |
| 5 | 2024-06-27 22:46:53.181455 | 2 | Variant | product_suggestion_click | {‘product_id’: 36} |
| 6 | 2024-06-07 21:34:37.181455 | 2 | Variant | session_start | {‘session_duration_in_sec’: 2126} |
| 7 | 2024-06-24 02:25:34.181455 | 2 | Variant | product_suggestion_click | {‘product_id’: 98} |
| 8 | 2024-06-12 02:03:44.181455 | 2 | Variant | product_suggestion_click | {‘product_id’: 45} |
| 9 | 2024-06-09 16:37:44.181455 | 2 | Variant | session_start | {‘session_duration_in_sec’: 2898} |
Analysis
Product Suggestion Clicks
When comparing metrics like clicks per user, time spent in the app, and revenue generated, we typically want to compare the mean or median in a given group. I most often use one of the following tests to check the significance of such differences:
- Student’s t-test (mean comparison) - if the data is normally distributed and the variances of the compared groups are equal,
- Welch’s t-test (mean comparison) - if the distribution is normal and the variances are not equal,
- Mann-Whitney U test (median comparison) - if the data does not meet the assumption of normality.
This means that the first step is always to check the normality of the distribution of the data being analyzed. The test I use most often to check for normality is the Shapiro-Wilk test. This is usually the preferred test because of its high sensitivity to deviations from normality, however it is also a bit computationally expensive, so if the number of observations being analyzed is large (e.g., hundreds of thousands) then the Kolmogorov-Smirnov test can also be used.
For statistical research purposes, we classically use the SciPy library. Here is a simple function that performs the Shapiro-Wilk normality test:
from scipy.stats import shapiro
def check_normality(data):
stat, p_value = shapiro(data)
is_normal = p_value > 0.05
result = {
"stat": stat,
"p value": p_value,
"is_normal?": is_normal
}
return result
Let’s extract the number of conversions per user from our data and check the normality of the distributions:
clicks_per_user = df[df['event_name'] == 'product_suggestion_click'].groupby(['user_id', 'test_group']).size().reset_index(name='click_count')
group_a_clicks = clicks_per_user[clicks_per_user['test_group'] == 'Baseline']['click_count']
group_b_clicks = clicks_per_user[clicks_per_user['test_group'] == 'Variant']['click_count']
result_a = check_normality(group_a_clicks)
result_b = check_normality(group_b_clicks)
result_c = check_normality(clicks_per_user['click_count'])
print("Baseline:", result_a)
print("Variant:", result_b)
The result of the operation is:
Baseline: {'stat': 0.9576061367988586,
'p value': 1.6581377937363584e-10,
'is_normal?': False}
Variant: {'stat': 0.9543760418891907,
'p value': 4.440712381148515e-11,
'is_normal?': False}
The null hypothesis in the Shapiro test is that the analyzed data has a normal distribution. Our p-values are much lower than the threshold value of 0.05, so there is no evidence that the distributions are normal, we reject the null hypothesis in favor of the alternative. To prove this visually, we can use a histogram.
import matplotlib.pyplot as plt
import seaborn as sns
plt.subplot(1, 2, 1)
sns.histplot(group_a_clicks, kde=True)
plt.title('Baseline')
plt.subplot(1, 2, 2)
sns.histplot(group_b_clicks, kde=True)
plt.title('Variant')
plt.show()
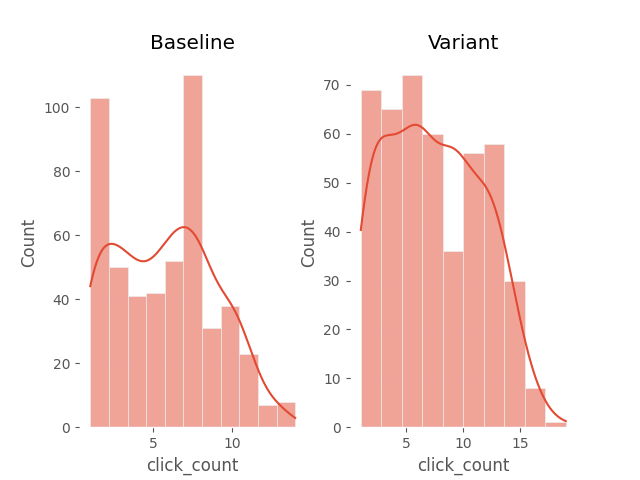 In both cases, the distribution is far from normal. Therefore, we need to use the non-parametric Mann-Whitney U test. This test is used to compare medians, so let’s check the medians of product suggestion clicks in both groups.
In both cases, the distribution is far from normal. Therefore, we need to use the non-parametric Mann-Whitney U test. This test is used to compare medians, so let’s check the medians of product suggestion clicks in both groups.
group_a_clicks.median()
group_b_clicks.median()
The result is 5 and 7, which seems like a significant difference. Let’s confirm using a statistical test whether this difference is not random.
from scipy.stats import mannwhitneyu
def mannwhitney_test(group_a, group_b):
stat, p_value = mannwhitneyu(group_a, group_b)
is_difference_significant = p_value < 0.05
result = {
"stat": stat,
"p value": p_value,
"is_difference_significant?": is_difference_significant
}
return result
result = mannwhitney_test(group_a_clicks, group_b_clicks)
print(result)
{'stat': 92221.5,
'p value': 3.6130679942676925e-08,
'is_difference_significant?': True}
The difference is statistically significant. The difference in medians between the product suggestion modules is 2 in favor of the new version of the solution.
User Session Duration
Average session duration per user is a frequently analyzed metric, providing insights into user engagement with applications. An increase in this duration when introducing new features suggests positive progress. To evaluate the significance of differences in this metric between two groups, I typically use the same tests as in the previous subsection.
Let’s construct data with average session durations per user and check the normality of distributions.
session_start_df = df[df['event_name'] == 'session_start']
avg_session_duration = session_start_df.groupby(['user_id', 'test_group'])['event_params'].apply(lambda x: np.mean([params['session_duration_in_sec'] for params in x])).reset_index()
avg_session_duration.rename(columns={'event_params': 'avg_session_duration_sec'}, inplace=True)
group_a_dur = avg_session_duration[avg_session_duration['test_group'] == 'Baseline']['avg_session_duration_sec']
group_b_dur = avg_session_duration[avg_session_duration['test_group'] == 'Variant']['avg_session_duration_sec']
result_a = check_normality(group_a_dur)
result_b = check_normality(group_b_dur)
print("Baseline result:", result_a)
print("Variant result:", result_b)
Baseline result: {'stat': 0.9958817362785339,
'p value': 0.21153901517391205,
'is_normal?': True}
Variant result: {'stat': 0.9958817362785339,
'p value': 0.21153901517391205,
'is_normal?': True}
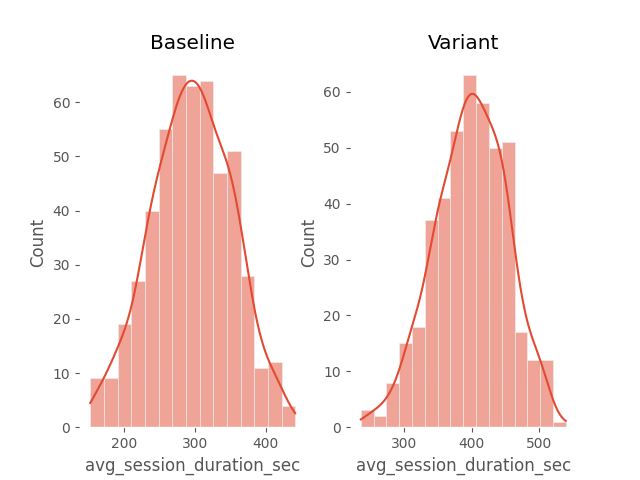
For both groups, the data distribution is normal. Let’s confirm this with histograms.
The next step is to compare the variances in both groups. If they are equal, we will use Student’s t-test, otherwise, Welch’s t-test. We will use Bartlett’s test for variance comparison.
from scipy.stats import bartlett
def bartlett_test(group_a, group_b):
stat, p_value = bartlett(group_a, group_b)
is_equal_variance = p_value > 0.05
result = {
"stat": stat,
"p value": p_value,
"is_equal_variance?": is_equal_variance
}
return result
result = bartlett_test(group_a_dur, group_b_dur)
print(result)
{'stat': 2.1164181551507277, 'p value': 0.14572700666267074, 'is_equal_variance?': True}
The p-value (0.146) is greater than 0.05, indicating that we cannot reject the null hypothesis of equal variances. Therefore, we can proceed with Student’s t-test for independent samples to compare the average session durations per user in both groups. The null hypothesis states that the means of both groups are equal.
from scipy.stats import ttest_ind
def t_test(group_a, group_b):
stat, p_value = ttest_ind(group_a, group_b)
is_difference_significant = p_value < 0.05
result = {
"stat": stat,
"p value": p_value,
"is_difference_significant?": is_difference_significant
}
return result
result = t_test(group_a_dur, group_b_dur)
print(result)
{'stat': -28.815699071086026, 'p value': 1.7993899138767928e-131, 'is_difference_significant?': True}
We reject the null hypothesis; the difference in average session durations per user between both groups is statistically significant. The mean for the old product suggestion module is ~295 seconds, whereas for the new one it is ~399 seconds. It is safe to conclude that the new functionality significantly impacts user engagement, potentially increasing the average session duration by up to 100 seconds.
Day 1 Retention
Day 1 retention is another metric describing user engagement with the application, specifically the percentage of users who return to the app on the day following their first use of the tested feature. To assess the significance of differences in such binary metrics (whether a user returned or not), I often use a Z-test for two proportions. The null hypothesis assumes no difference between the proportions being studied. Let’s begin by preparing a function that checks whether a user registered a session on the next day after their first product suggestion click. The function will return a dataframe with a boolean field indicating this situation. Next, we’ll split the table into two data series for the test groups.
def calculate_day1_retention_per_user(df):
first_click_df = df[df['event_name'] == 'product_suggestion_click'].sort_values(by=['user_id', 'event_date']).drop_duplicates(subset=['user_id'], keep='first')
first_click_df['next_day'] = first_click_df['event_date'] + pd.to_timedelta(1, unit='d')
session_start_df = df[df['event_name'] == 'session_start']
merged_df = pd.merge(first_click_df, session_start_df, how='left',
left_on=['user_id', 'test_group', 'next_day'],
right_on=['user_id', 'test_group', 'event_date'],
suffixes=('', '_y'))
merged_df['day1_retention'] = ~merged_df['event_name_y'].isna()
retention_df = merged_df[['user_id', 'test_group', 'day1_retention']]
return retention_df
retention_df = calculate_day1_retention_per_user(df)
group_a_ret = retention_df[retention_df['test_group'] == 'Baseline']['day1_retention']
group_b_ret = retention_df[retention_df['test_group'] == 'Variant']['day1_retention']
Now we can prepare a function that will perform the Z-test. The test is not mathematically complex, but we can use an implementation from the statsmodels package.
from statsmodels.stats.proportion import proportions_ztest
def proportions_test(group_a_len, group_a_suc_count, group_b_len, group_b_suc_count):
stat, p_value = proportions_ztest([group_a_suc_count, group_b_suc_count], [group_a_len, group_b_len])
is_difference_significant = p_value < 0.05
result = {
"stat": stat,
"p value": p_value,
"is_difference_significant?": is_difference_significant
}
return result
Let’s calculate the total number of users and those who returned to the app the next day for both groups and perform the test.
group_a_len = len(group_a_ret)
group_b_len = len(group_b_ret)
group_a_suc_count = group_a_ret[group_a_ret==True].count()
group_b_suc_count = group_b_ret[group_b_ret==True].count()
result = proportions_test(group_a_len, group_a_suc_count, group_b_len, group_b_suc_count)
print(result)
{'stat': -4.008891563617293, 'p value': 6.1004419366713936e-05, 'is_difference_significant?': True}
A very low p-value was obtained, leading to rejection of the null hypothesis. The difference between the proportions studied is statistically significant. Approximately 11% of users from the baseline group returned to the app the next day after their first use of the product suggestion feature. For the variant group, this rate was approximately 21.7%. Thus, it can be said that implementing the new feature positively impacts retention; in the test conditions, the difference exceeds 10 percentage points. Of course, in the real world, it would be worth considering whether studying day 1 retention is logical for a shopping application, as people do not typically plan to shop daily. It would be valuable to examine different time intervals.
Summary
The A/B test analysis is complete. As a data analyst, I would return to the product manager or the person responsible for the enhanced product suggestion feature with the following conclusions:
- Users are interacting with the new version of the functionality more frequently, with a difference in the median conversion rate per user of 2.
- The new functionality has an impact on user engagement with the app, with the average session duration per user increasing by nearly 35%.
- Users with the new version of the functionality are more likely to return to the app the next day, with the Day 1 retention rate difference exceeding 10 percentage points.
We can confidently say that the new version of the product suggestion module is a success. It can be rolled out to all users, as the differences are significant. However, it is essential to continue monitoring the data. Every change introduces a novelty effect, so it’s crucial to check whether the metrics decline over time. Of course, the functionality should continue to be improved. If the differences in the studied metrics were statistically insignificant, I would likely suggest continuing the test and increasing the sample size. If the results were reversed, it would be concerning, and we would need to dig deeper, possibly through error analysis or user feedback.
I hope you found this post interesting. Of course, in real life, things are never so straightforward. More scenarios should be considered, and more metrics analyzed. Data never aligns so perfectly, and changes rarely have such significant effects. Sometimes, we fight for growth in the decimal fractions of a percent. The most important thing is that new functionalities or changes to existing ones are tested, and decisions are made based on correctly analyzed data. See you in the next post!